Well, I've been reading a lot of Asian-pacific news lately, and one thing I've noticed is a lot of emphasis (especially in China) on designing "greener" buildings and hybrid, high gas mileage vehicles. Cool science aside on these designs, I can't help but think of the nasty effect these seemingly environmentally conscious ideas have on the environment due to Jevon's paradox. Now, for those of you who haven't taken macro econ. 202, Jevon's paradox states the following:
"As technological improvements increase the efficiency with which a resource is used, total consumption of that resource may increase, rather than decrease."
I've been in Thailand for over a month now and I've occasionally mentioned how smoggy it is here. The question I initially ask is: "How can the entire country of Thailand be smoggier than ANY city in America (even Detroit), when America started the industrial revolution and has had so much more time to get smoggy?" Well, a partial answer is; fuel-efficient motorcycles. Motorcycles made personal transport much more available to the general public, and you motorcycle riders out there recognize the greatly increased gas mileage of motorcycles. That means, even though each individual motorcycle produces less emissions than an average sized car, the value of the motorcycle's efficiency makes it attractive to more people in the population, shifting the supply graph to the right, and increasing the total quantity of resource used.

So even though Thailand has only been automotivally developing since the mid-1970s, it has already made the air around the cities nearly incompatible with human life. I'm not saying that because I'm some sort of huge wuss, the smog is officially serious and globally life-threatening.

More in line with Jevon's paradox, when the motorcycle became available to the people of thailand, do you think total petroleum consumption went down, or up? If you guessed up, you're right! And what is the primary petroleum expenditure in Thailand?

Transportation! Now, with that micro example out of the way, let's look at the total growth in Thailand's economy over the last four years...7.5% growth.
Wow, like everyone is saying, Asia is growing like crazy right now. Okay, so what does 7.5% growth mean? Well, its an exponential function, and so I'm going to teach you a fun little equation you can use to track the total use of any resource, its called, doubling time!" Only I won't use that annoying wikipedia equation, we'll just delve into the simplified world of natural log (ln).
The time it takes for a sample to be doubled in size based on constant growth can be summed up in the following equation:
Doubling time (years) = (ln 2)/(yearly growth rate)
But ln2 = 0.693, so we can multiply everything by 100 and get this equation:
Doubling time = 70/x%
So if the growth of the entire Thailand economy as determined by petroleum usage grows by 7.5% yearly, then the time it takes for the total petroleum usage for Thailand to double is approximately 70/7.5 = 9.33 years.
That's right, the size of Thailand's economy (as determined by petroleum usage) doubles every 9.33 years. And it doesn't matter what your sample size is, doubling is doubling based only on percentage growth rate, so if we start at 5 "units", the first doubling time makes the total 10 units, the second doubling time makes the total 20 units, the third doubling time makes the total 40 units, etc. etc. etc. So if we assume Thailand's smog level is directly proportional to petroleum useage, you can see how in just under three decades smog levels have gotten so fricking thick. Every single doubling time uses as many resources as every doubling time before it combined (by definition)!
You can apply that function to anything that has a steady growth rate, like, population; (average growth rate since 1800 AD is ~2%)
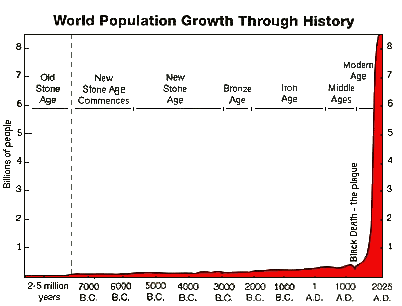
Oil consumption; (average growth rate ~5% annually)

Deer population in Iowa; (1.7% annually)

Vampire populations;

You get the idea. Of course yearly growth rates fluctuate from year to year with anything, but you can use this formula to predict steadily rising sample sizes. So whenever a local paper brags that the cities growth is the highest ever, and the mayor expects equal growth the next year, you can get a rough estimate what kind of impact such growth will have and how long it will take.
To bring this all back to Jevon's paradox, as the technology that uses a resource becomes more efficient, those resources become available to more people, and more resources are used per capita, which increases growth rate (decreasing doubling time), and increases total resources used! But these designers are trying to reduce total resources used! Ack! Paradox!
So, what do we have in store for Conservation speeds Collapse Part 2? I haven't figured that out yet. Looks like we're doomed!